CS:APP Chapter 5 Summary ⚡

March 26, 2022

Recently, I’ve been studying CS:APP - I’m posting my own summary of chapter 5 that I wrote up using Notion.

Chapter 5 : Optimizing Program Performance

5.1 Capabilities and Limitations of Optimizing Compilers

Safe Optimizations

Compilers must apply only safe optimizations to a program.

Safe optimization means that resulting program will have the exact same behavior as would an unoptimized version for all possible cases the program may encounter.

Optimization blockers

Optimization blockers
Optimization blockers are aspects of programs that can severely limit the opportunities for a compiler to generate optimized code.

Memory Aliasing
Two pointers may designate the same memory location.
```
void twiddle1(long *xp, long *yp){ //requires 6 memory references
	*xp += *yp;
  *xp += *yp;
}

void twiddle2(long *xp, long *yp){ //requiers only 3 memory references
	*xp += 2 * *yp;
}
```
If xp and yp are equal, function twiddle1 and twiddle2 will have different result.
In performing only safe optimizations, the compiler must assume that different pointers may be aliased.

Function calls
Functions have a side effect if it modifies some part of the global program state.
```
long f();

long func1(){
	return f() + f() + f() + f();
}

long func2(){
  return f() * 4;
}
```
It seems like func1 and func2 would have identical results, but if f has a side effect, two functions will work differently.
```
long counter = 0;

long f(){
	return counter++;
}
```
Most compilers don’t try to determine whether a function is free of side effects. Instead, compilers assumes the worst case and leaves function calls intact.

5.2 Expressing Program Performance

CPE
CPE, cycles per element, is the metric we use to express program performance.
Many procedures contain a loop that iterates over a set of elements.
The time required by such a procedure can be characterized as a constant + a factor proportional to the number of elements processed.
We refer to the coefficients in the terms as the effective number of cycles per element.
example : If run time is approximated by 60 + 35n, CPE is 35.

5.3 Program Example

Vector Data Structure

We will use a running example based on the vector data structure shown below.

/*Create abstract data type for vector */
typedef struct {
	long len;
	data_t *data; //data_t can be either int, long, float, or double.
} vec_rec, *vec_ptr;

Basic Procedures

We use some basic procedures shown below for generating vectors, accessing vector elements, and determining the length of a vector.

Generating vectors

/* Create vector of specified length */
vec_ptr new_vec(long len){
	/* Allocate header structure */
	vec_ptr result = (vec_ptr) malloc(sizeof(vec_rec));
  data_t *data = NULL;
	if (!result) return NULL; //Couldn't allocate storage
	result->len = len;
	
	/* Allocate array */
	if (len > 0){
		data = (data_t *) calloc(len, sizeof(data_t));
		if(!data){
			free((void*) result);
			return NULL; //Couldn't allocate storage
		}
	}
	/* Data will be NULL or allocated array */
	result->data = data;
	return result;
}

Accessing vector elements

/* Retrieve vector element and store at dest. */
/* Return 0 (out of bounds) or 1 (successful) */
int get_vec_element(vec_ptr v, long index, data_t *dest){
	if(index < 0 || index >= v->len) return 0; //bounds checking
	*dest = v->data[index];
	return 1;
}

Determining the length of a vector

long vec_length(vec_ptr v){
	return v->len;
}

Combine1

combine1 combines all of the elements in a vector into a single value according to some operation.

void combine1(vec_ptr v, data_t *dest){
	long i;

	*dest = IDENT;
	for (i = 0; i < vec_length(v); i++){
		data_t val;
		get_vec_element(v, i, &val);
		*dest = *dest OP val;
	}
}

OP and IDENT are compile-time constants. combine1 can compute different values as OP and IDENT are defined differently.

#define IDENT 0
#define OP +
//combine1 will sum the elements of the vector.

#define IDENT 1
#define OP *
//combine1 will product the elements of the vector.

We will proceed through a series of transformations of the code, writing different versions of the combining function.

Measuring CPE performance
We measured the CPE performance of the functions on a machine with an Intel Core i7 Haswell processor, which we refer to as our reference machine.
- CPE measurements for combine1 running on our reference machine.
Function Method Integer + Integer * Floating Point + Floating Point *
combine1 Abstract unoptimized 22.68 20.02 19.98 20.18
combine1 Abstract -O1 10.12 10.12 10.17 11.14
As we can see, by simply giving the command-line option -O1, enabling a basic set of optimizations, we can improve the program performance significantly.

5.4 Eliminating Loop Inefficiencies

combine2 : Improving the inefficiency of the loop test
combine1 calls function vec_length as the test condition of the for loop.
The test condition must be evaluated on every iteration of the loop, whereas the length of the vector doesn’t change as the loop proceeds.
We could therefore compute the vector length only once and use this value in the test condition.
```
void combine2(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); //compute vector length only once
	
	*dest = IDENT;
	for(i = 0; i < length; i++){
		data_t val;
		get_vec_element(v, i, &val);
		*dest = *dest OP val;
  }
}
```
- Performance Improvement
This transformation has noticeable effect on the overall performance for some data types and operations, and minimal or even none for others.
Function Method Integer + Integer * Floating Point + Floating Point *
combine1 Abstract -O1 10.12 10.12 10.17 11.14
combine2 Move vec_length 7.02 9.04 9.02 11.03

Code Motion
- Code motion
  Code motion involves identifying a computation that is performed multiple times, but such that the result of the computation will not change.
  We can move the computation to an earlier section of the code that doesn’t get evaluated as often.
- Code motion and compiler
  Compilers can’t reliably detect whether or not a function will have side effects, so they are typically very cautious about making transformations that change where or how many times a procedure is called.
  Therefore, the programmer must often help the compiler by explicitly performing code motion.

Another Example of Loop Inefficiency : lower1 and lower2
```
void lower1(char *s){
	long i;
	for(i = 0; i < strlen(s); ++i)
		if (s[i] >= 'A' && s[i] <= 'Z') s[i] -= ('A' - 'a');
}

void lower2(char *s){
	long i;
	long len = strlen(s); //compute length of string only once
	for(i = 0; i < len; ++i)
		if (s[i] >= 'A' && s[i] <= 'Z') s[i] -= ('A' - 'a');
}
```
strlen takes time proportional to the length of string. ( $O(n)$ )
Since strlen is called in each of the n iterations of lower1, the overall run time of lower1 is proportional to $n^2$ . ( $O(n^2)$ )
On the other hand, since lower2 only calls strlen once, the overall run time of lower2 is proportional to $n$ . ( $O(n)$ )

5.5 Reducing Procedure Calls

Reducing Procedure Calls
Procedure calls can incur overhead and also block most forms of program optimization. We can reduce unnecessary procedure calls to optimize the overall performance.

combine3 : Eliminating function calls within the loop
```
data_t *get_vec_start(vec_ptr v){
	return v->data;
}

void combine3(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); 
	data_t *data = get_vec_start(v); // get starting address of data array

	*dest = IDENT;
	for(i = 0; i < length; i++){
		*dest = *dest OP data[i]; // access directly to the element
  }
}
```
Since all references of data array in combine are valid, we can eliminate the function calls in the inner loop.
- Performance Improvement
Surprisingly, there is no apparent performance improvement. (Check 5.11)
Function Method Integer + Integer * Floating Point + Floating Point *
combine2 Move vec_length 7.02 9.04 9.02 11.03
combine3 Direct data access 7.17 9.02 9.02 11.03

5.6 Eliminating Unneeded Memory References

Unnecessary Memory references in combine3
- x86-64 code of inner loop of combine3 (data_t = double, OP = *)
Accumulated value is read from and written to memory on each iteration. (Line 2, 4)
Since the value read from dest at the beginning of each iteration should simply be the value written at the end of the previous iteration, this reading and writing is wasteful.

combine4 : Accumulating result in temporary
```
void combine4(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); 
	data_t *data = get_vec_start(v);
	data_t acc = IDENT;	// hold accumulated value in local var acc

	for(i = 0; i < length; i++){
		acc = acc OP data[i]; // accumulate result in acc
  }
}
```
By eliminating unneeded memory reference in combine3, we have reduced the memory operations per iteration from 2 reads and 1 write to just a single read.
- Performance Improvement
There is a significant improvement in program performance.
Function Method Integer + Integer * Floating Point + Floating Point *
combine3 Direct data access 7.17 9.02 9.02 11.03
combine4 Accumulate in temporary 1.27 3.01 3.01 5.01

Different behaviors between combine3 and combine4
combine3 and combine4 can behave differently due to memory aliasing.
- Example of memory aliasing
Let v = [2, 3, 5], and consider following two function calls :
```
combine3(v, get_vec_start(v) + 2);
combine4(v, get_vec_start(v) + 2);
```
We create an alias between the last element of the vector and the destination for storing the result. The two functions would execute as follows :
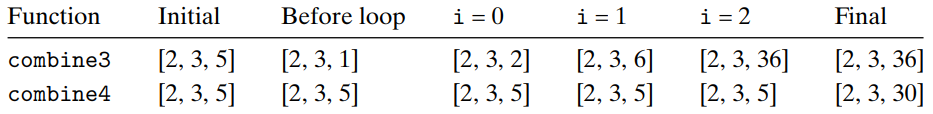
Since combine3 and combine4 can behave differently in corner cases like this, compiler can’t automatically transform combine3 to accumulate the value in a register.

combine3w : compiler’s optimization for combine3
```
void combine3w(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); 
	data_t *data = get_vec_start(v);
	data_t acc = IDENT;

	/* Initialize in event length <= 0 */
	*dest = acc;

	for(i = 0; i < length; i++){
		acc = acc OP data[i];
		*dest = acc; // make sure dest updated on each iteration
  }
}
```
When we use GCC to compile combine3 with command-line option -O2, we get x86-64 code of optimized version that operates much like the C code above.
In this optimization, combine3w will operate same even when memory aliasing occurs because location dest is updated on each iteration.

5.7 Understanding Modern Processors

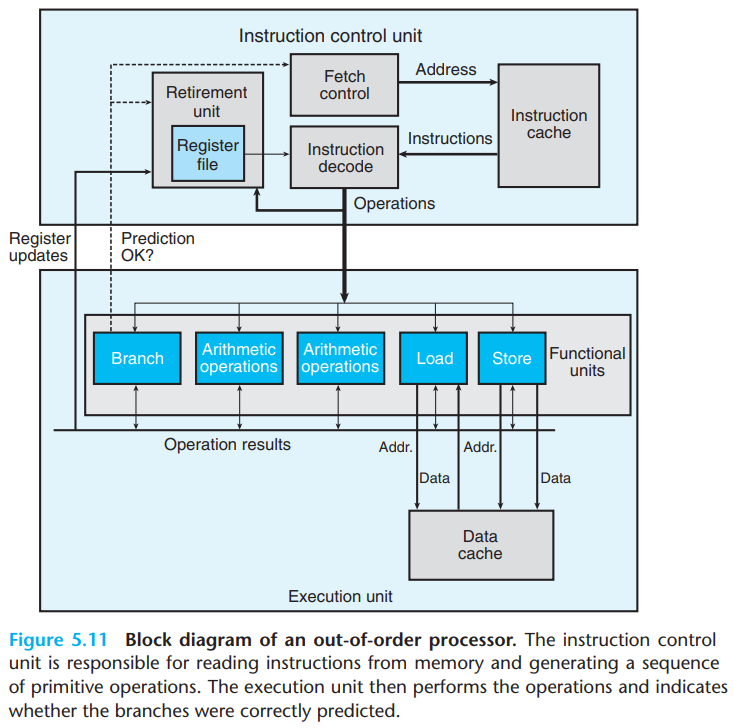
Overall Operation
- Superscalar & Out of Order
  Our hypothetical processor are superscalar and out of order.
  Superscalar processors can perform multiple operations on every clock cycle.
  For processors that are out of order, the order in which instructions execute need not correspond to their ordering in the machine-level program.
- ICU(Instruction Control Unit)
  ICU is responsible for reading a sequence of instructions from memory and generating a set of primitive operations from the instructions to perform on program data.
  - Instruction Cache
  ICU reads the instructions from an instruction cache - a special high-speed memory containing the most recently accessed instructions.
  - Fetch Control
  Modern processors employ branch prediction - they guess whether or not a branch will be taken and also predict the target address for the branch.
  Using a technique known as speculative execution, the processor begins fetching, decoding instructions, and executing these operations at where it predicts the branch will go, before it has been determined whether or not the branch prediction was correct.
  The block labeled “Fetch Control” incorporates branch prediction.
  - Instruction Decode
  The instruction decoding logic takes the actual program instructions and converts them into a set of primitive operations.
  For example, in a typical x86 implementation, an instruction addq %rax, 8(%rdx) yields multiple operations. - one to load a value from memory into the processor, one to add the loaded value to the value in %eax, and one to store the result back to memory.
  - Retirement Unit
  The retirement unit keeps track of the ongoing processing and makes sure that it obeys the sequential semantics of the machine-level program. The retirement unit controls the updating of register file.
  The detailed description of retirement unit will be discussed below.
- EU (Execution Unit)
  EU receives a number of operations from the instruction fetch unit on each clock cycle, then executes the primitive operations.
  - Functional Units
  Received operations are dispatched to a set of functional units that perform the actual operations.
  - Functional Units - Load and store units
  Load and store units handle operations that read data from memory into the processor, and operations that write data from the processor to the memory respectively.
  Load and store units have an adder to perform address computations.
  Load and store units access memory via a data cache, a high speed memory containing the most recently accessed data values.
  - Functional Units - Branch unit
  Branch operations are sent to EU, to determine whether or not the prediction was correct.
  If prediction was incorrect → EU will discard the computed results beyond the branch point, signal the branch unit that the prediction was incorrect, and indicate the correct branch destination. → Branch unit begins fetching at the new location.
  Such a misprediction incurs a significant cost in performance.
  - Functional Units - Arithmetic units
  The arithmetic units perform different combinations of integer and floating point operations.
  The arithmetic units are intentionally designed to be able to perform a variety of different operations, since the required operations vary widely across different programs.
  For example, Intel Core i7 Haswell reference machine has 8 functional units. Here is a partial list of each one’s capabilities:
  0. Integer arithmetic, floating-point multiplication, integer and floating-point division, branches
  1. Integer arithmetic, floating-point addition, integer multiplication, floating point multiplication
  2. Load, address computation
  3. Load, address computation
  4. Store
  5. Integer arithmetic
  6. Integer arithmetic, branches
  7. Store address computation
  This combination of functional units has the potential to perform multiple operations of the same type simultaneously. (For example, it has 4 units capable of performing integer operations.)
- Retirement & Flush
  As an instruction is decoded in ICU, information about it is placed into a queue. This information remains in the queue until 2 outcomes occurs :
  - Retirement
  The operations have completed and any branch points leading to this instruction are confirmed as being correctly predicted → The instruction can be retired, with any updates to the program registers being made.
  - Flush
  Some branch point leading to this instruction was mispredicted → The instruction will be flushed, discarding any results that may have been computed.
- Exchanging Operation results
  To expedite the communication of results from one instruction to another, much of this information is exchanged among the execution units, shown in the figure as Operation results. This is a more elaborate form of the data-forwarding technique.
  - Register Renaming
  Register renaming is one of the most common mechanism for controlling the communication of operands among the execution.
  When an instruction that updates register r is decoded, a tag t is generated giving a unique identifier to the result of the operation. An entry (r, t) is added to a table maintaining the association between program register r and tag t for an operation that will update register r. When a subsequent instruction using register r as an operand is decoded, the operation sent to the execution unit will contain t as the source for the operand value.
  When some execution unit completes the first operation, it generates a result (v, t), indicating that the operation with tag t produced value v. Any operation waiting for t as source will then use v as the source value, a form of data forwarding.
  Using register renaming, values can be forwarded directly from one operation to another, rather than being written to and read from the register file. Also, an entire sequence of operations can be performed speculatively, even though the registers are updated only after the processor is certain of the branch outcomes.

Functional Unit Performance - Latency bound and Throughput bound
- Latency : the total time required to perform the operation
- Issue time : the minimum number of clock cycles between two independent operations of the same type
- Capacity : the number of functional units capable of performing that operation
The addition and multiplication operations all have issue times of 1 → The processor can start a new one of these operations on each clock cycle. This short issue time is achieved through the use of pipelining. Functional units with issue times of 1 cycle are said to be fully pipelined.
Divider is not pipelined(its issue time equals its latency) → the divider must perform a complete division before it can begin a new one.
- Throughput : reciprocal of the issue time, the number of operations executed on each clock cycle
For an operation with capacity C and issue time I, the processor can achieve a throughput of C/I operations per clock cycle. (example : our reference machine can perform floating-point multiplication at a rate of 2 per clock cycle.)
- Latency bound
Latency bound gives a minimum value for the CPE for any function that must perform the combining operation in a strict sequence.
- Throughput bound
Throughput bound gives a minimum bound for the CPE based on the maximum rate at which the functional units can produce results.
- Examples
There is only one integer multiplier having an issue time of 1 clock cycle → the processor can’t sustain a rate of more than 1 multiplication per clock cycle.
With four integer adder, the processor can sustain a rate of 4 operations per cycle. However, two load units limit the processor to reading at most 2 data values per clock cycle → yields throughput bound of 0.5.

An Abstract Model of Processor Operation
CPE measurements obtained for combine4 match the latency bound for the processor, except for the case of integer addition. → The performance of these functions is dictated by the latency of the sum or product computation.
- From Machine-Level Code to Data-Flow Graphs
We will visualize how the data dependencies in a program dictate its performance using data-flow graph of combine4. Since the computation performed by the loop is the dominating factor in performance for large vectors, we focus just on this.
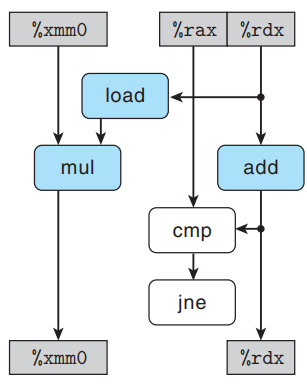
Four instructions are expanded into a series of 5 operations, with the initial multiplication instruction being expanded into a load operation and a mul operation.
Some of the operations in data-flow graph produce values that do not correspond to registers - load reads a value from memory and passes it directly to mul, and cmp updates the condition codes, which are then tested by jne.
For a code segment forming a loop, we can classify the registers that are accessed into 4 categories:
- Read-only
These are used as source values, either as data or to compute memory addresses, but they are not modified within the loop. (example : %rax in combine4)
- Write-only
These are used as the destinations of data-movement operations.
- Local
These are updated and used within the loop, but there is no dependency from one iteration to another. (example : condition code registers in combine4)
- Loop
These are used both as source values and as destinations for the loop, with the value generated in one iteration being used in another. (example : %rdx, %xmm0 in combine4)
The chains of operations between loop registers determine the performance-limiting data dependencies.
In data-flow graph, white colored operators indicate that they are not part of some dependencies between loop registers.
(example : cmp and jne operations in combine4. We assume that checking branch condition can be done quickly enough that it doesn’t slow down the processor.)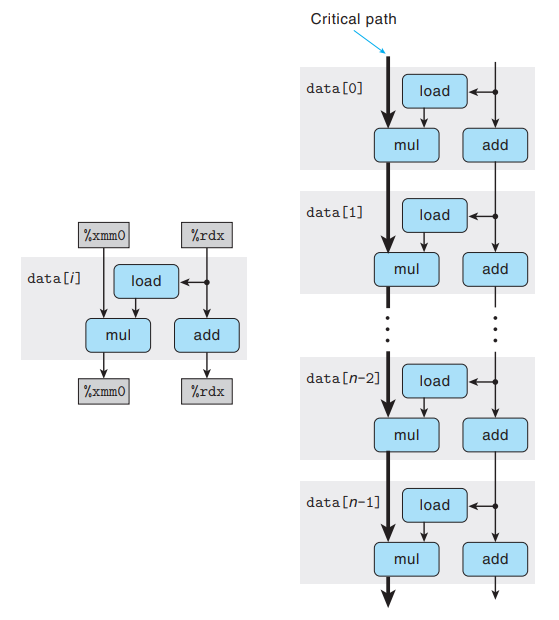
In more simplified data-flow graph, the operators that were colored white are eliminated, retaining only the loop registers.
Along one side, we see the dependencies between successive values of program value acc, stored in register %xmm0. The loop computes a new value for acc by multiplying the old value by a data element, generated by the load operation.
Along the other side, we see the dependencies between successive values of the pointer to the ith data element. On each iteration, the old value is used as the address for the load operation, and it is also incremented by the add operation to compute its new value.
As we see the data-flow representation of n iterations by the inner loop of combine4, we can see that the program has two chains of data dependencies, corresponding to the updating of acc and data+i with operations mul and add.
Floating-point multiplication has a latency of 5 cycles, while integer addition has a latency of 1 cycle → The chain on the left will form a critical path, requiring 5n cycles to execute.
The other operations required during the loop proceed in parallel with the multiplication.
For other combinations of data type and operation where the operations has a latency L greater than 1, the measured CPE is simply L → This chain forms the performance-limiting critical path.
- Other Performance Factors
For integer addition, our measurements of combine4 show a CPE of 1.27, slower than the 1.00 → The critical paths in a data-flow representation provide only a lower bound on how many cycles a program will require.
Other factors can also limit performance, including the total number of functional units available, and the number of data values that can be passed among the functional units
We can restructure the operations to enhance instruction-level parallelism, so that our only limitation becomes the throughput bound.

5.8 Loop Unrolling

Loop Unrolling
Loop unrolling is a program transformation that reduces the number of iterations for a loop by increasing the number of elements computed on each iteration.
Loop unrolling improves performance by reducing the number of operations that do not contribute directly to the program result, (example : loop indexing, conditional branching) and exposing ways to further transform the code to reduce the number of operations in critical path.
To do k * 1 loop unrolling, we do following things :
- Set the upper limit to be n - k + 1.
- Within the loop, apply the combining operation to elements i through i + k - 1.
- Loop index i is incremented by k in each iteration.
- Include second loop to step through the final few elements of the vector.
Since this transformation unrolls by a factor of k but accumulate values in a single variable acc, it’s called k * 1 loop unrolling.

combine5 : Applying 2 * 1 Loop Unrolling

/* 2 X 1 loop unrolling */
void combine5(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); 
	long limit = length - 1;
	data_t *data = get_vec_start(v);
	data_t acc = IDENT;

	/* Combine 2 elements at a time */
	for(i = 0; i < limit; i+=2){
		acc = (acc OP data[i]) OP data[i+1]; // accumulate result in acc
  }

	/* Finish any remaining elements */
	for (; i < length; i++){
		acc = acc OP data[i];
	}
	*dest = acc;
}

Performance Improvement

Function	Method	Integer +	Integer *	Floating Point +	Floating Point *
`combine4`	No unrolling	1.27	3.01	3.01	5.01
`combine5`	2 * 1 unrolling	1.01	3.01	3.01	5.01
	3 * 1 unrolling	1.01	3.01	3.01	5.01

Loop unrolling reduced the number of overhead operations relative to the number of additions for computing vector sum → Integer addition reached its latency bound too.

Why k * 1 Loop Unrolling Can’t Improve Performance Beyond the Latency Bound
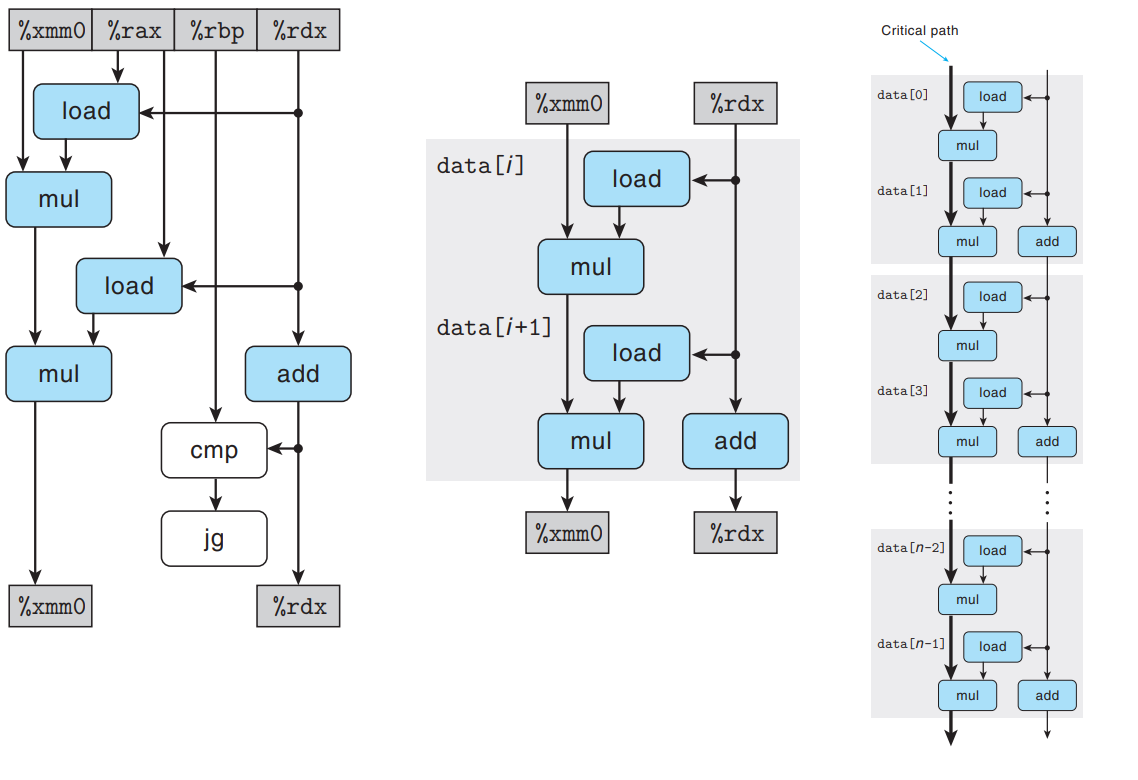
The loop unrolling leads to two vmulsd instructions - one to add data[i] to acc, and the second to add data[i+1] to acc.
We see that %xmm0 gets read and written twice in each execution of the loop. → If we execute one iteration n/2 times, there is still a critical path of n mul operations.

5.9 Enhancing Parallelism

combine6 : Multiple Accumulators - 2 * 2 Loop Unrolling
We can improve performance by splitting the set of combining operations and combining the results at the end for a operation that is associative and commutative.
For example, let $P_n$ denote the product of elements of $a_n$ : $P_n=\prod_{i=1}^{n-1}{a_i}$
Then, $P_n=PE_n\times PO_n$ , where $PE_n=\prod_{i=0}^{n/2-1}{a_{2i}}$ and $PO_n=\prod_{i=0}^{n/2-1}{a_{2i+1}}$ .
combine6 uses both two-way loop unrolling to combine more elements per iteration, and two-way parallelism by accumulating elements with even indices in acc0 and elements with odd indices in acc1. → 2 * 2 Loop Unrolling
```
/* 2 X 2 loop unrolling */
void combine6(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); 
	long limit = length - 1;
	data_t *data = get_vec_start(v);
	data_t acc0 = IDENT;
	data_t acc1 = IDENT;

	/* Combine 2 elements at a time */
	for(i = 0; i < limit; i+=2){
		acc0 = acc0 OP data[i];
		acc1 = acc1 OP data[i+1];
  }

	/* Finish any remaining elements */
	for (; i < length; i++){
		acc0 = acc0 OP data[i];
	}
	*dest = acc0 OP acc1;
}
```
- Performance Improvement
Function Method Integer + Integer * Floating Point + Floating Point *
combine5 2 * 1 unrolling 1.01 3.01 3.01 5.01
combine6 2 * 2 unrolling 0.81 1.51 1.51 2.51
The barrier imposed by the latency bound is broken!
- Data-flow graph of combine6
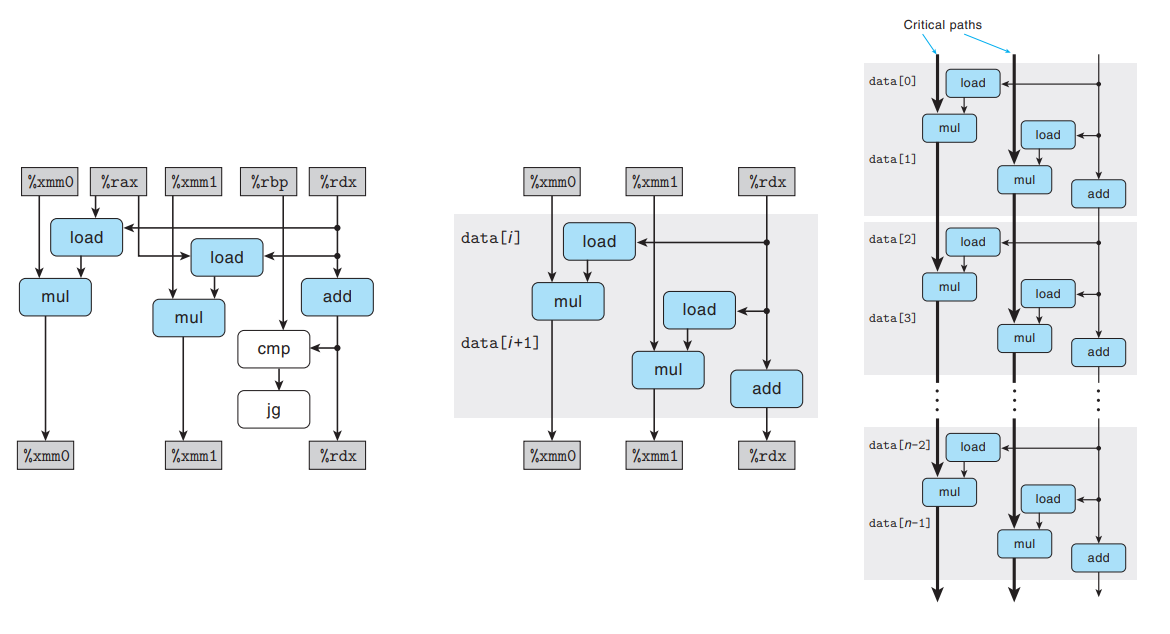
As with combine5, combine6 contains two vmulsd operations, but there is no dependency between them. → We now have two critical paths, one corresponding to computing the product of acc0 and one for acc1.
If we execute one iteration n/2 times, each of these critical paths contains only n/2 operations, leading to a CPE of around 5.00/2 = 2.50.
A similar analysis explains our observed CPE of around L/2 for operations with latency L.
Programs are exploiting the capabilities of the functional units to increase their utilization by a factor of 2.

k * k Loop Unrolling
We can generalize the transformation to unroll the loop by a factor of k and accumulate k values in parallel, yielding k * k loop unrolling.
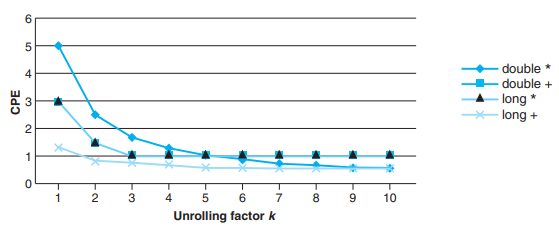
All of the CPEs improve with this transformation, achieving near their throughput bounds.
In general, a program achieve the throughput bound only when it can keep the pipelines filled for all functional units capable of performing that operation - For an operation with latency L and capacity C, this requires an unrolling factor $k \ge C*L$ .
- k * k Loop Unrolling’s Side effect
Integer addition and multiplication is commutative and associative - The result computed by combine6 will be identical to that computed by combine5 for all possible conditions.
Floating-point multiplication and addition are not associative - combine6 could produce different results with combine5.
For example, if $a_n$ ’s element with even indices are very large, and those with odd indices are very close to 0.0, $PE_n$ might overflow or $PO_n$ might underflow, even though computing $P_n$ proceeds normally.
Therefore, some compilers do k * k loop unrolling or similar transformation on integer operations, while most compilers don’t attempt such transformations with floating-point code.

combine7 : Reassociation Transformation - 2 * 1a Loop Unrolling
```
/* 2 X 1a loop unrolling */
void combine7(vec_ptr v, data_t *dest){
	long i;
	long length = vec_length(v); 
	long limit = length - 1;
	data_t *data = get_vec_start(v);
	data_t acc = IDENT;
	
	/* Combine 2 elements at a time */
	for(i = 0; i < limit; i+=2){
		acc = acc OP (data[i] OP data[i+1]);
  }

	/* Finish any remaining elements */
	for (; i < length; i++){
		acc = acc OP data[i];
	}
	*dest = acc;
}
```
combine7 differs from combine5 only in the way the elements are combined in inner loop : acc = (acc OP data[i]) OP data[i+1]; to acc = acc OP (data[i] OP data[i+1]);.
We call this transformation as reassociation transformation, since the parentheses shift the order the vector elements are combined with acc, yielding 2 * 1a loop unrolling.
- Performance Improvement
Function Method Integer + Integer * Floating Point + Floating Point *
combine5 2 * 1 unrolling 1.01 3.01 3.01 5.01
combine6 2 * 2 unrolling 0.81 1.51 1.51 2.51
combine7 2 * 1a unrolling 1.01 1.51 1.51 2.51
Most cases match the performance of combine6, breaking through the barrier imposed by the latency bound.
- Data-flow graph of combine7
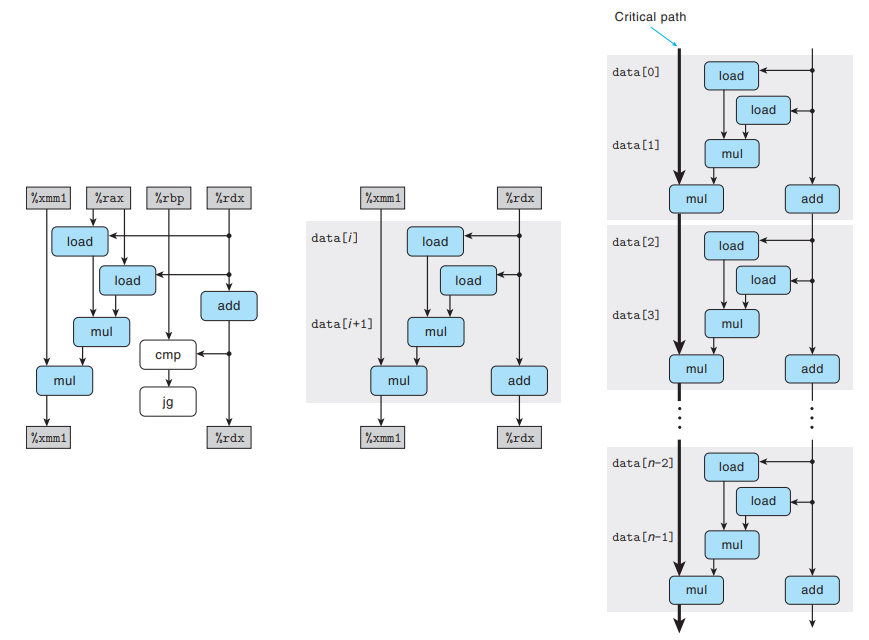
As with combine5, combine6 contains two vmulsd operations - the first mul multiplies data[i] and data[i+1], and the second multiplies the result by acc.
However, only one of the mul operations forms a data-dependency chain between loop registers - the first multiplication within each iteration can be performed without waiting for the acc from the previous iteration. → We reduce the minimum CPE by a factor of 2.

k * 1a Loop Unrolling
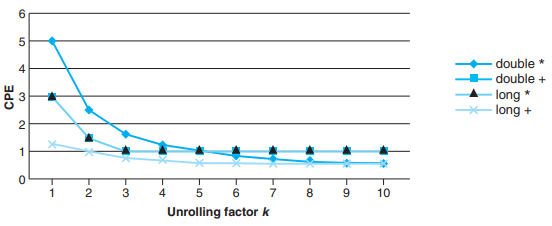
k * 1a loop unrolling yields performance results similar to k * k loop unrolling, all of CPEs achieving near their throughput bounds.
- k * 1a Loop Unrolling’s Side effect
Since reassociation transformation changes the order of operations, k * 1a loop unrolling might have a different result for non-associative operations. (example : float-point codes)
Therefore, most compilers won’t attempt any reassociations of floating-point operations.
- k * 1a Loop Unrolling vs. k * k Loop Unrolling
In general, k * k loop unrolling is a more reliable way to achieve improved program performance.

5.10 Summary of Results for Optimizing Combining Code

By using multiple optimizations, we have been able to achieve CPEs close to the throughput bounds of 0.5 and 1.00, limited only by the capacities of the functional units.

5.11 Some Limiting Factors

Register Spilling
If a program has a degree of parallelism P that exceeds the number of available registers, then the compiler will resort to spilling, storing some temporary values in run-time stack.
- Example : 10 * 10 loop unrolling & 20 * 20 loop unrolling
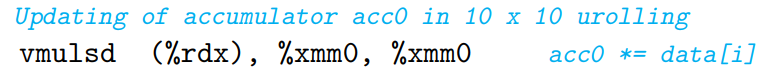
Once a compiler must resort to register spilling, the advantage of maintaining multiple accumulators will most likely to be lost.

Branch Prediction and Misprediction Penalties
Misprediction penalty is incurred when the processor discard all of the speculatively executed results and restart the instruction fetch process at the correct location.
How can a C programmer reduce branch misprediction penalties?
1. Do Not Be Overly Concerned about Predictable Branches
The branch prediction logic of modern processors is very good at discerning regular patterns and long-term trends for the different branch instructions.
(example : 5.5’s combine3 has no apparent performance improvement because processor is already able to predict outcomes of the branch.)
1. Write Code Suitable for Implementation with Conditional Moves
For unpredictable cases, program performance can be enhanced if the compiler can generate code using conditional data transfers, rather than conditional control transfers.
GCC can generate conditional moves for code written in a more functional style - use conditional operations to compute values and then update the program state with these values. (↔imperative style - use conditionals to selectively update program state)
- example : minmax1(imperative) vs. minmax2(functional)
```
/* Rearrange two vectors so that for each i, b[i] >= a[i] */
void minmax1(long a[], long b[], long n){
	long i;
	for (i = 0; i < n; i++){
		if(a[i] > b[i]){
			long t = a[i];
			a[i] = b[i];
			b[i] = t;
		}
	}
}

void minmax2(long a[], long b[], long n){
	long i;
	for (i = 0; i < n; i++){
		long min = a[i] < b[i] ? a[i] : b[i];
		long max = a[i] < b[i] ? b[i] : a[i];
		a[i] = min;
		b[i] = max;
	}
}
```
Not all conditional behavior can be implemented with conditional data transfers, however, programmers can sometimes make code more amenable to translation into conditional data transfers.

5.12 Understanding Memory Performance

Load / Store Functional Unit
Modern processor’s functional units for load and store operations have internal buffers to hold sets of requests for memory operations.
Our reference machine has two load units, each of which can hold up to 72 pending read requests, and one store unit with a store buffer containing up to 42 write requests.

Load Performance
To determine the latency of the load operation on a machine, we set up a computation with a sequence of load operations as below :
```
/* Linked List */
typedef struct ELE { 
	struct ELE *next;
	long data;
} list_ele, *list_ptr;
/* Return Length of Linked List */
long list_len(list_ptr ls){
	long len = 0;
	while (ls) {
		len++;
		ls = ls->next;
	}
	return len;
}
```
- Assembly code for the loop
The load operation on line 3 forms the critical bottleneck in the loop - the load operation for one iteration can’t begin until one for the previous iteration has completed.
The measured CPE of list_len is 4.00 - matches the documented access time of 4 cycles for the reference machine’s L1 cache.

Store Performance
In most cases, store operation can operate in a fully pipelined mode, and doesn’t affect any register values - Only a load operation is affected by the result of a store operation.
```
/* Write to dest, read from src */
void write_read(long* src, long *dst, long n){
	long cnt = n;
	long val = 0;
	
	while(cnt) {
		*dst = val;
		val = (*src) + 1;
		cnt--;
	}
}
```
If src and dst point to same memory space, each load by *src will yield the value stored by the previous execution of *dst. (example : write_read(&a[0], &a[0], 3))
This example illustrates write/read dependency - the outcome of a memory read depends on a recent memory write.
Write/read dependency leads to significant loss of performance - write_read(&a[0], &a[1], 3)'s CPE is measured as 1.3, while write_read(&a[0], &a[0], 3)'s CPE is measured as 7.3.
- Detail of load and store units
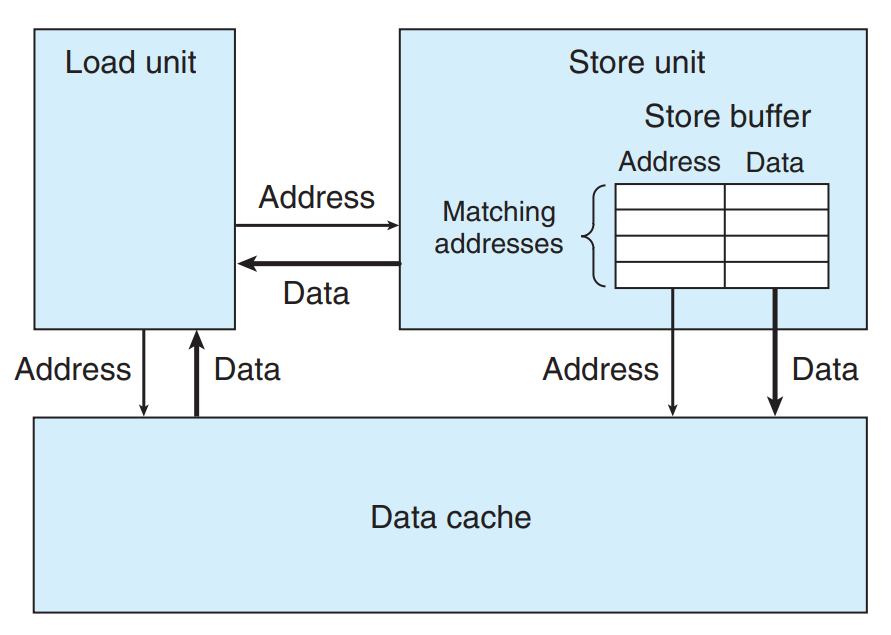
The store unit includes a store buffer containing the address and data of the store operations that have been issued to the store unit, but have not yet been completed.
When a load operation occurs, it must check the entries in the store buffer for matching addresses - If it finds a match, it retrieves the corresponding data entry as the result of the load operation.
- Data-flow graph of write_read
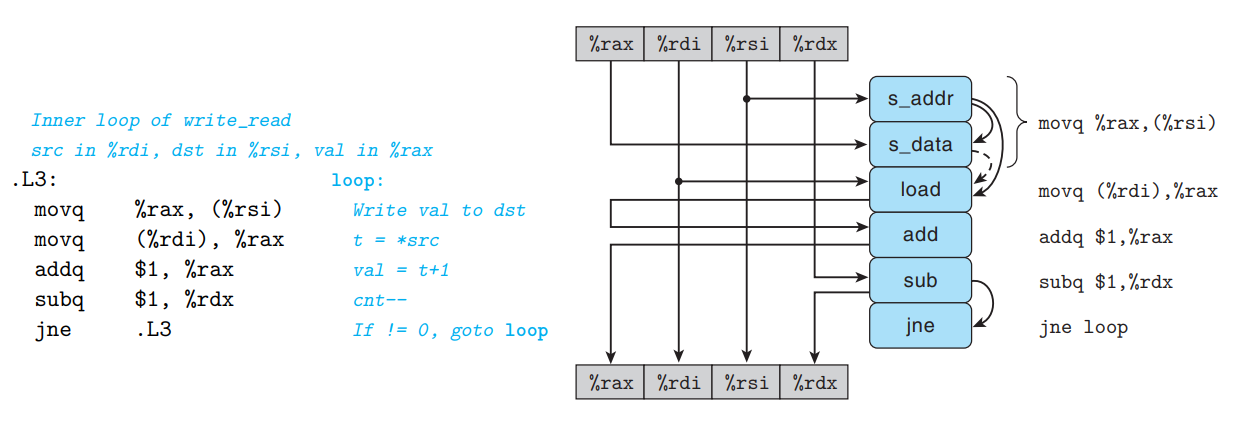
movq %rax, (%rsi) is translated into two operations: s_addr computes the address for the store operation, creates an entry in the store buffer, and sets the address field for that entry. s_data sets the data field for the entry.
There can be 3 data dependencies between operations within inner loop of write_read :
1. s_addr → s_data
The address computation of the s_addr must precede s_data.
1. s_addr → load
load generated by decoding movq (%rdi), %rax must check the addresses of any pending store operations.
1. s_data → load (only when load and store addresses match)
If two addresses match, load must wait until s_data has deposited its result into the store buffer.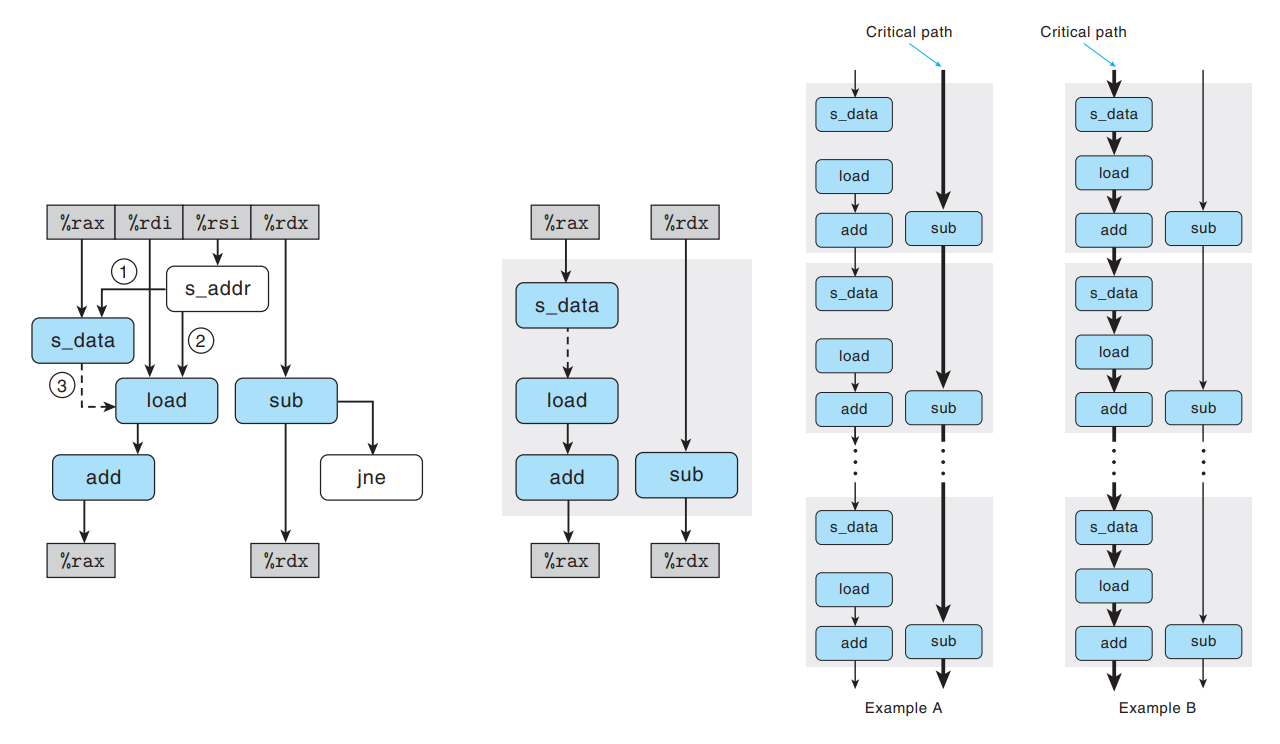
Data-flow graph of write_read shows two chains of dependencies : one with data values being stored, loaded, and incremented (only for the case of matching addresses); and the one decrementing variable cnt.
With differing source and destination addresses, load and store can proceed independently → only critical path is formed by the decrementing of cnt, resulting in a CPE bound for 1.0.
With matching source and destination addresses, data dependency between s_data and load causes a critical path → these three operations in sequence require a total of around 7 clock cycles.

5.13 Life in the Real World: Performance Improvement Techniques

Basic strategies for optimizing program performance

High-level design

Choose appropriate algorithms and data structures.

Basic coding principles : Avoid optimization blockers
- Eliminate excessive function calls.
- Move computations out of loops when possible.
- Eliminate unnecessary memory references.

Low-level optimizations
- Unroll loops to reduce overhead and to enable further optimizations.
- Find ways to increase instruction-level parallelism by multiple accumulators and reassociation.
- Rewrite conditional operations in a functional style to enable compilation via conditional data transfers.

Avoid introducing errors as you rewrite programs in the interest of inefficiency.

5.14 Identifying and Eliminating Performance Bottlenecks

When working with large programs, even knowing where to focus our optimization efforts can be difficult → use code profilers, analysis tools that collect performance data about a program as it executes!

Profiler helps us focus our attention on the most time-consuming parts of the program and also provides useful information about the procedure call structure.

In general, profiling can help us optimize for typical cases, assuming we run the program on representative data, but we should also make sure the program will have respectable performance for all possible cases.

Share on

Twitter Facebook LinkedIn

Woo hyuk Choi